Index
Lecture4
note: Lecture 3 is about Linear Algebra review, check at the end of “week2 note” for more info.
Note for Coursera Machine Learning made by Andrew Ng.
Multiple features
We still use the previous examp;e (house price pridiction problem). Then we add the following notations for convenience.
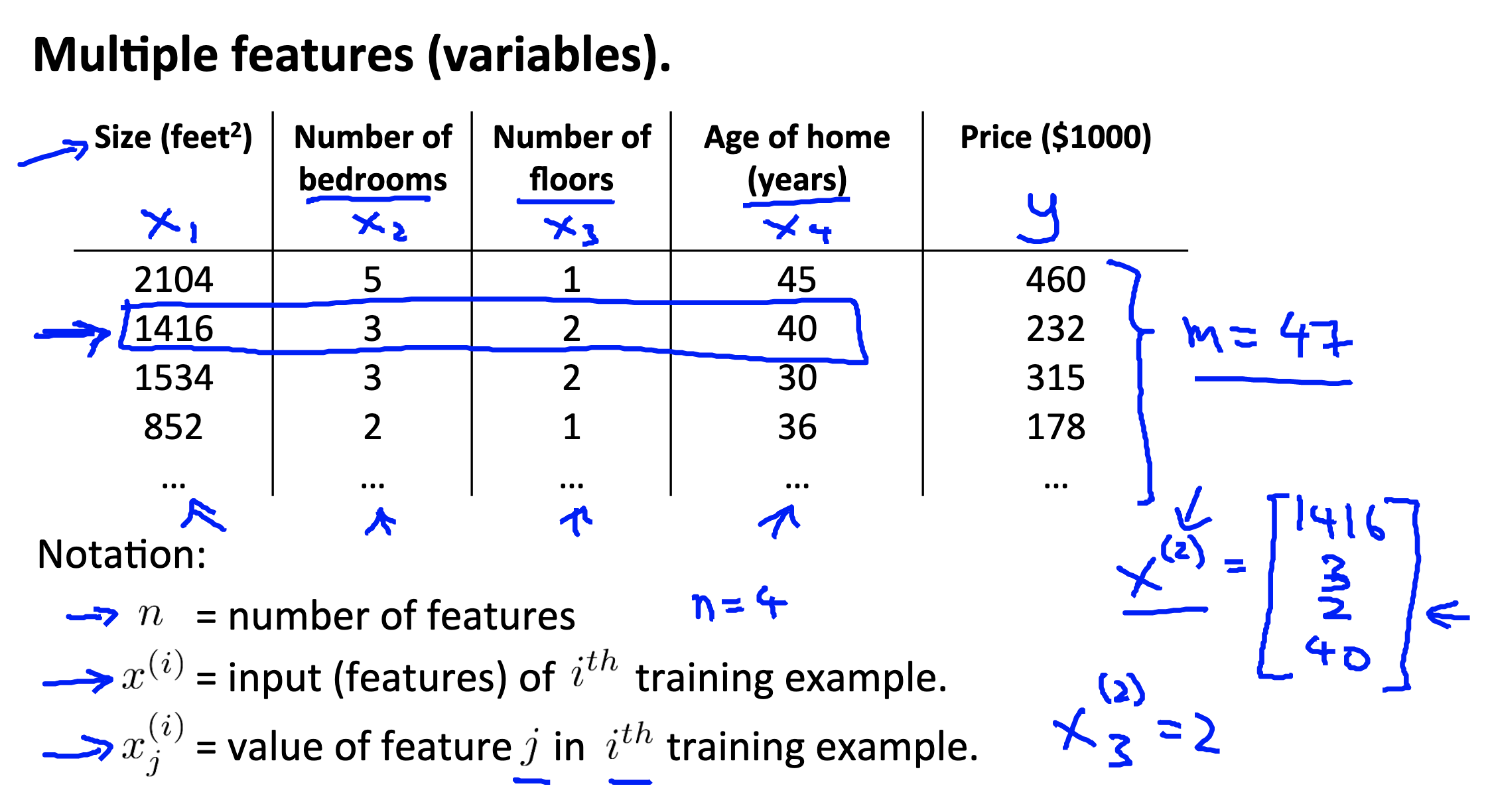
Notations
= number of features. = input (features) of training example. = value of feature in training example.
Because the hypothesis is defined as
Which is equal to
We can then represent the hypothesis in martix form
Link to coursera section
Gradient descent for multiple variables

Below is the proof I did for better understand the vectorized gradient descent
Link to coursera section
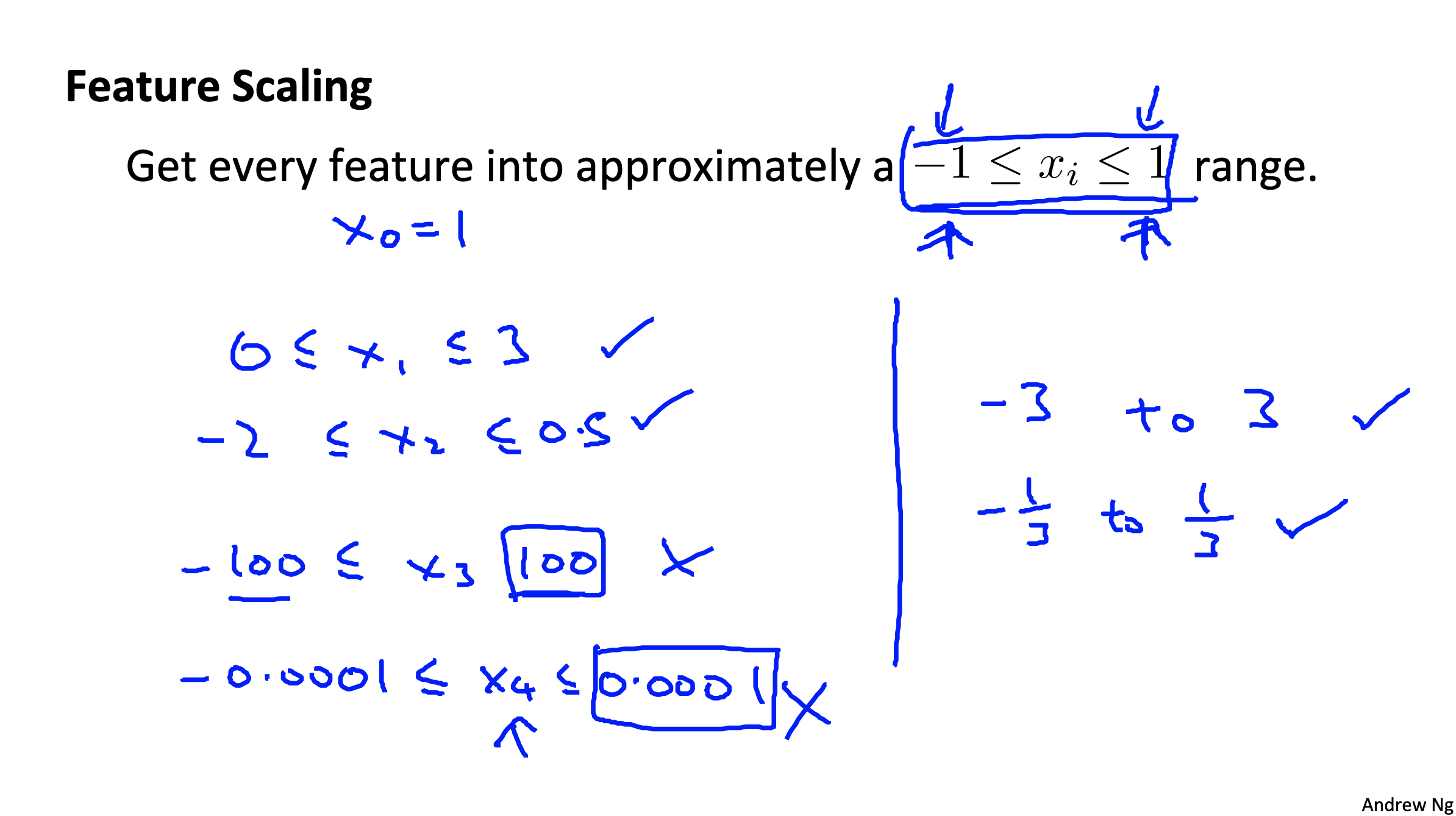
Gradient descent in practice I: Feature Scaling
The purpose of Feature Scaling is to speedup gradient descent
- Idea: Make sure features are on a similar scale. (eg. see as below)
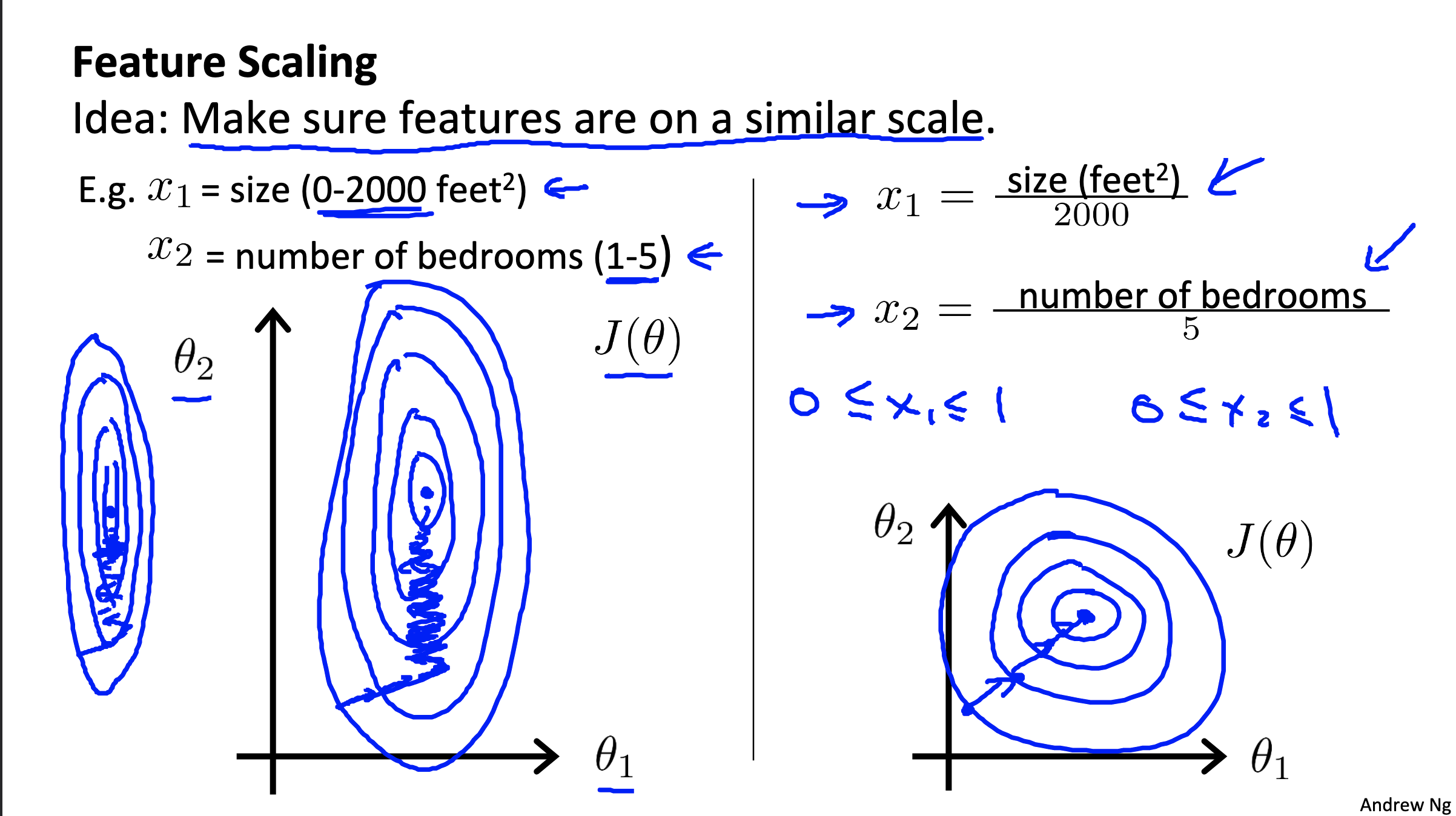
We can see from above figure that the gradient requires a lot more iterations to approch the minimum point if features are no on a similar scale.
Mean normalization
This is a technic which normalize the range (optimze gradient descent)
details see the figure below:
Link to coursera section
Gradient descent in practice II: Learning rate

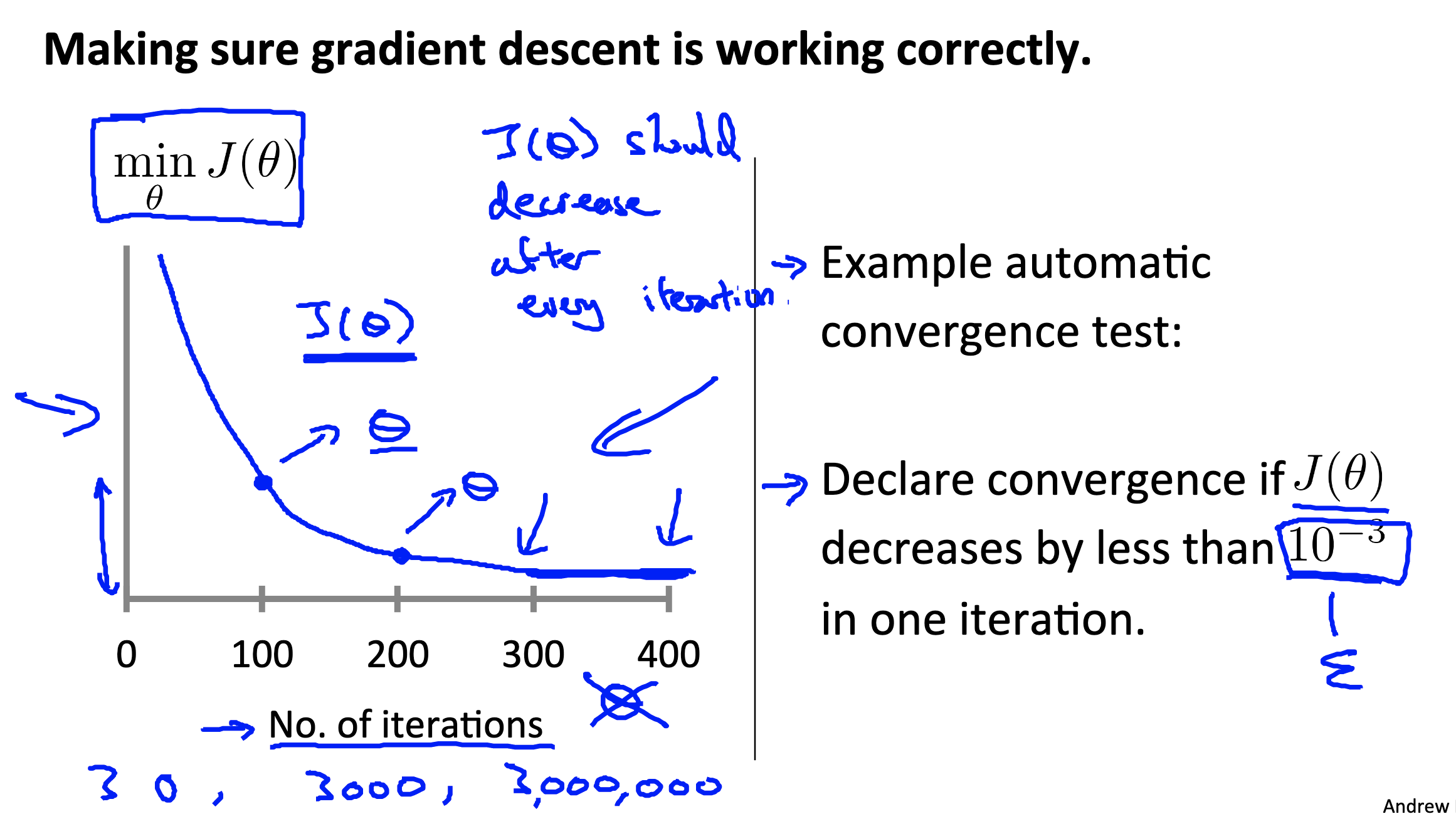
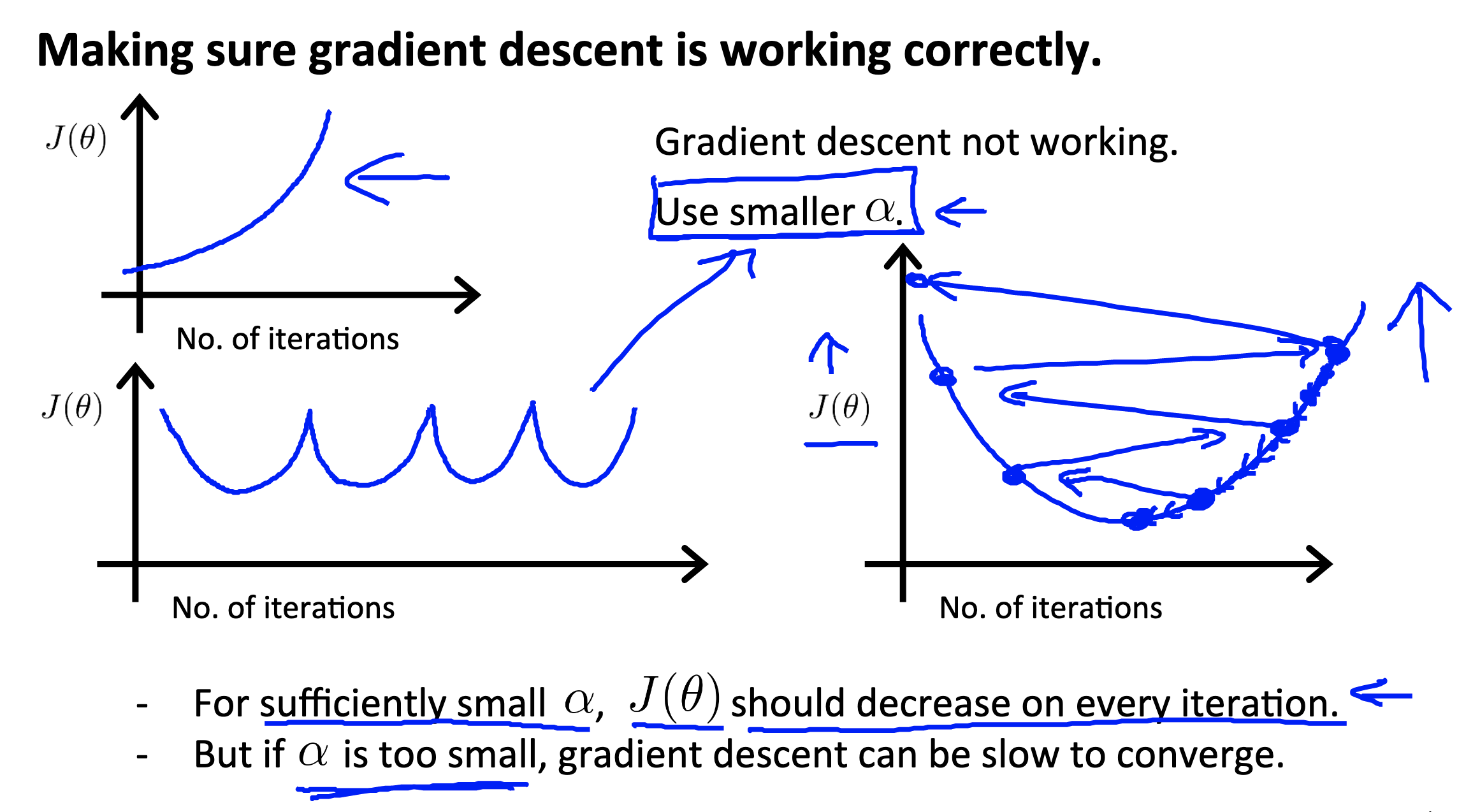

Link to coursera section
Features and polynomial regression
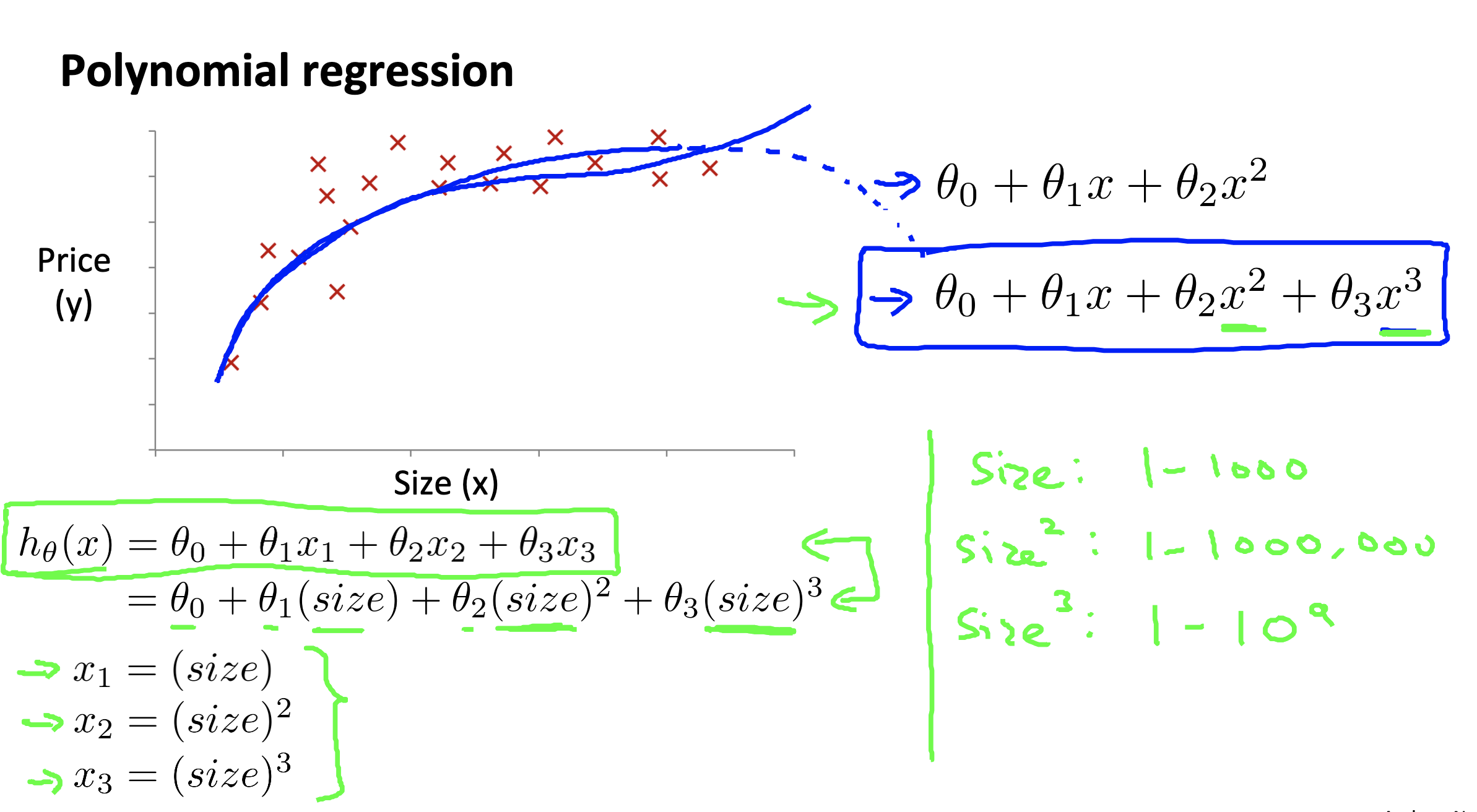
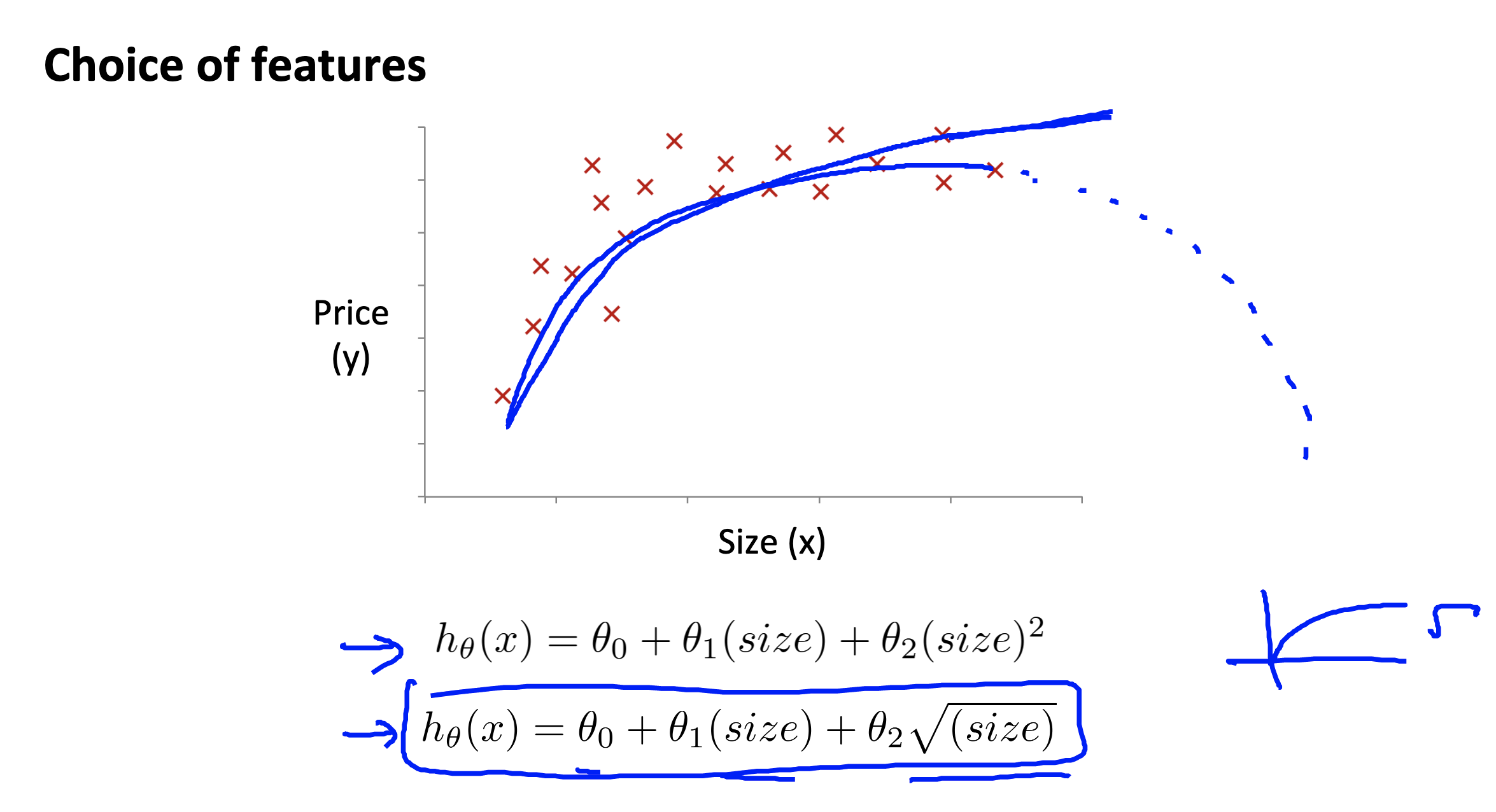
Link to coursera section
Normal equation
Normal equation is a method to solve for
Proof see below
Comparison between gradient descent & normal equation

Link to coursera section
Normal equtaion and non-invertibility
- In Ocatave/Matlab, we use pinv(pseudo inverse) instead of inv. So it is rare that we can’t find the inverse of
Useful links
- Pseudo-inverse: https://www.youtube.com/watch?v=pTUfUjIQjoE
- Generalized_inverse(synonym of Moore–Penrose inverse): https://en.wikipedia.org/wiki/Generalized_inverse
- Reason of using pinv instead of inv (eg. when matrix in singular):https://stats.stackexchange.com/a/69459
What if
