Main topics in the lecture
[TOC]
Material used
UCL COMP0012 regex.pdf : https://moodle.ucl.ac.uk/pluginfile.php/3383507/mod_resource/content/2/regex.pdf
COMP0012 Note by (Joe Xu, Henry Zhang, Felix Hu, Davies Xue, John Xu):
https://github.com/jieyouxu/COMP0012-Compilers-Notes
Lexemes
Definition (Lexeme): A lexeme is a contiguous sequence of characters that form a lexical unit in the grammar of a language
(Intuitively, a lexeme is a “word” and defined by delimiters, like space in English)
Caution! Terminological Confusion in this Module
Just some justifies. (will not appear in the exam)
 "
"
(examples of token type (token in CS term))
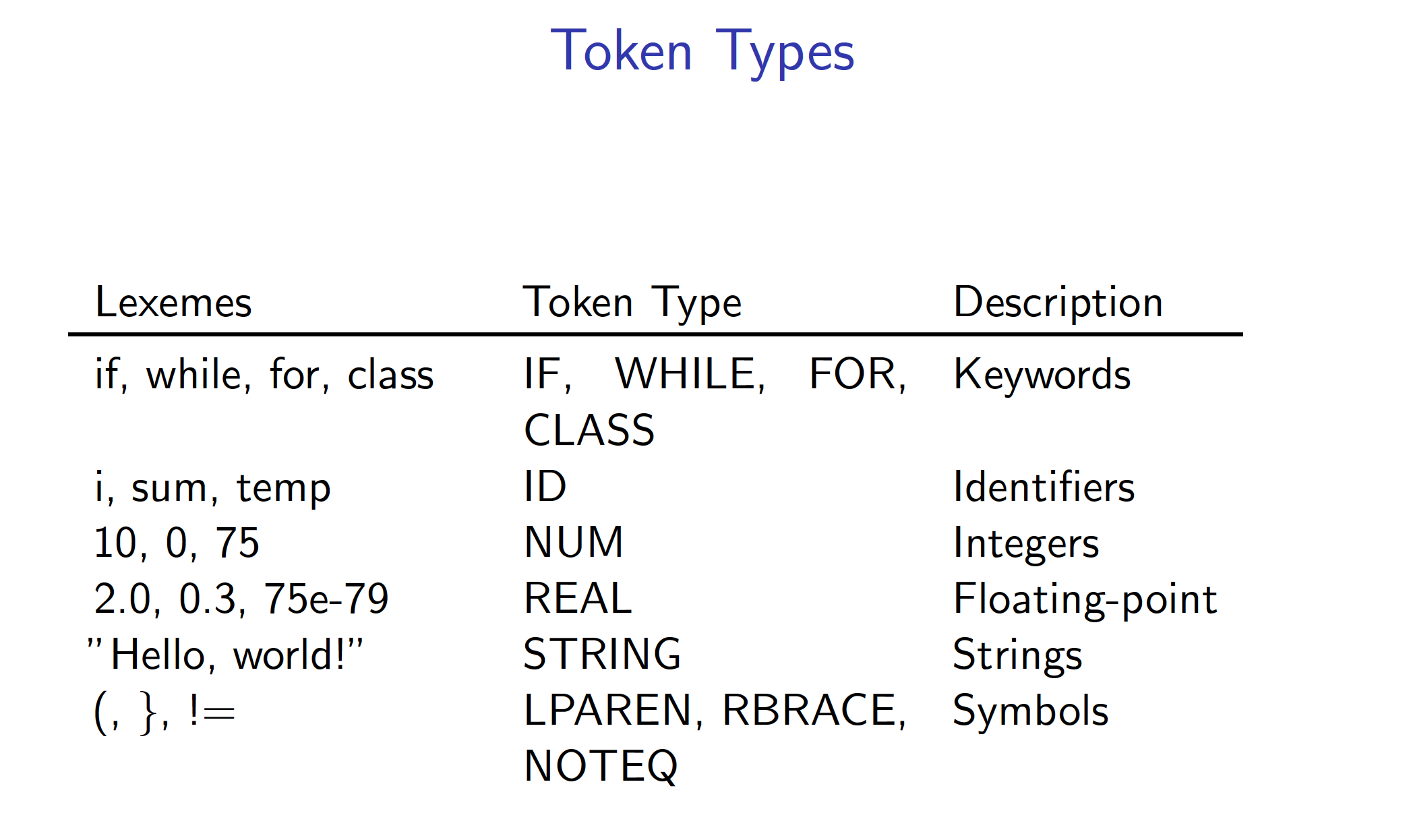
- := is referential equality
- = Math equality (== in programming language)
Another Eg.
1 | int i, sum; |
Describing and Recognizing Lexemes
- Describing Lexemes
- An Anonymous Language Standard
- An identifier is a sequence of letters and digits, starting with a letter. Upper and lower case letters are different. The underscoure _ counts as a letter.
We use regular expresstions to specify lexemes
- Recognizing Lexemes
Finite State Automata, or Machines (FSA or FSM) are used to recognise the lexemes described by regular expressions
Definition of a Language
- An alphaet
is a finite set of symbols. - A string over
is a contiguous sequence of symbols from
Definition (Language)
A language is a set of strings over some
Regular Expressions
Regular Operations
For the languages
UNION is often written
Regular Expression Formal Definition
For the alphabet
Where
Remark. Note that parentheses are need for the inductive cases to prevent
ambiguity. This definition assumes that the concatenation, union and
Kleene star operators have equal precedence.
Examples



Associativity
Parentheses are tedious to write and distracting to read.
Operator priority:
So
Synactic Sugar
(Syntax Sugar). Syntax sugar for regexes are introduced
as aliases to make the regular language easier to express. However, syntax
sugars do not otherwise change the expressiveness of regular languages –
they are simply aliases.

Remark. Operators introduced means there is a need to escape the metacharacters,
the characters which themselves are used to represent the regular
operators.
For example, to use the meta-character ∣ as an input character for a
regular expression, one could escape it as |.

Ambiguity
Definition
An regular expression is ambiguous if it recognizes an input in more than one way
Eg. (00)(000) recognizes 000000 in two ways
- 000 - 000
- 00 - 00 - 00
Eg2. A more significant example would be in the case of keywords vs
identifiers in a programming language
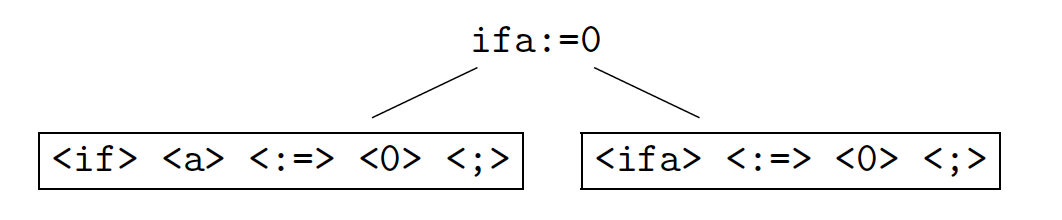
ID and IF overlap: HOW we decide which to use?
Disambiguation
- Longest Match
- Rule priority, typically order
Greedy Matching
Greedy matching refers to the default
behaviour for regexes to recognize as much of the input as possible
eg.
Say you want to match tags, as shown in the box:
$\fbox {< a href=”http://www.utopia.com" > } Visit utopia <\a>$
if you write <
$\fbox {< a href=”http://www.utopia.com > “ Visit utopia <\a>}$
$\fbox {< a href=”http://www.utopia.com" > }Visit utopia \fbox {<\a>}$
Searching vs. Lexing
Searching seeks to find a substring that satisfies a regular expression and can ignore the rest of its input, while lexing must recognize all of its input.
Any search, like /abc/, trivially becomes a lex when bracketed with
.*, i.e. /.abc./, if it succeeds.
Remark. Note that while searching aims to find a substring which matches
the supplied regex, lexing aims to find all substrings which matches the
supplied regex.
Perl Compatible Regular Expression (PCRE)
Regex is not the same as PCRE. In industry, they usually mean PCRE as regular expression.
- Capture groups
(abc){3} matches “abcabcabc”. The first group matches “abc”
- Back references
(abc | def) =\1 matches abc=abc or def=def, but not abc=def or def=abc
(Requires backtracking)
- Newline-aware
- Named groups
- Subroutines
- Atomic grouping
- Recursion: /^(a(?1)?b)
a^nb^n$ - Qualifiers
- Control longest vs shortest match.
PCRE useful info
for test and learn RegEX: https://regexr.com/
Useful youtube link: https://www.youtube.com/watch?v=rhzKDrUiJVk
Online tutorial(Runoob_CH): https://www.runoob.com/regexp/regexp-tutorial.html